4104. Distance in tree
A connected
graph without cycles is called a tree.
The distance
between two vertices of a tree is defined as the length (in edges) of the
shortest path between these vertices.
Given a tree with
n vertices and a positive integer k. Compute the number of distinct pairs
of vertices of the tree whose distance is equal to k. Note that pairs (v, u)
and (u, v) are considered the same
pair.
Input. The first line contains two integers n and k (1
≤ n ≤ 50000, 1 ≤ k ≤ 500) – the
number of vertices in the tree and the required distance between vertices.
The next n – 1
lines
contain the edges of the tree in the format ai bi (1 ≤ ai, bi ≤ n, ai ≠ bi), where ai and bi are the vertices of
the tree connected by the i-th edge.
All specified edges are different.
Output. Print a
single integer – the number of distinct pairs of tree vertices whose distance is
equal to k.
|
Sample
input |
Sample
output |
|
5 2 1 2 2 3 3 4 2 5 |
4 |
SOLUTION
dynamic programming - tree
Algorithm analysis
Let dp[v][x] be the number of
vertices at distance x from vertex v in the subtree rooted at v.
Set dp[v][0] = 1, considering that there
is only one vertex v at the distance 0 from itself. Let vertex v have sons u1, u2, .., up. Then
dp[v][x] = ![]()
The number of
vertices at distance x from vertex v (in the subtree rooted at v) is equal to the number of vertices at
distance x – 1 from the children of vertex v.
Let’s consider the
subtree rooted at v. We’ll count how
many paths of length k exist within it that pass through vertex v. Divide them
into two groups:
·
paths that start at v. Their number is dp[v][k].
·
paths that pass through v and have their endpoints in the subtrees of the children of v.
Consider a path
of length k passing through the root of subtree v. Let the distance from v
to one of its ends be x, where 1 ≤ x ≤ k – 1 (for example,
this end is located in the subtree with root u1). Then the
distance from v to the other end is k – x (the second end may be located in any other subtree different
from the subtree rooted at u1).
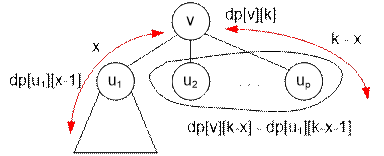
If the distance
from the first end of the path to v
is x, then the distance from it to u1 is x – 1. The number of
ways to choose this end is dp[u1][x – 1]. The number of
ways to choose the second end of the path is equal to the number of vertices
located at distance k – x from v, but not lying in the subtree rooted
at u1. Their number is dp[v][k
– x] – dp[u1][k – x – 1]. According to the multiplication rule, the number of such
paths is dp[u1][x – 1] * (dp[v][k – x] – dp[u1][k – x – 1]).
Thus, their
number is
dp[v][k] + ![]()
We just need to
sum up the given
expression over all vertices.
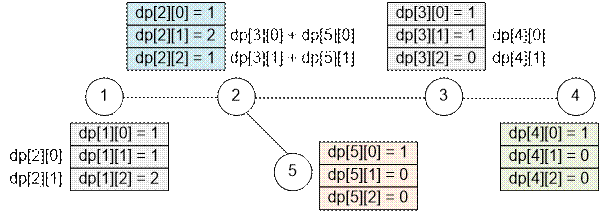
Example
Let’s consider the
tree provided in the example.
Algorithm realization
The array g
contains the tree. The dp array is used for dynamic programming.
vector<vector<int> > g;
vector<vector<int> > dp;
The dfs function implements depth-first search from vertex v. The value p is the parent of v. Construct the array dp.
void dfs(int
v, int p = -1)
{
Initialize the array dp[v].
dp[v].resize(k+1);
dp[v][0] = 1;
for(int i = 0; i < g[v].size(); i++)
{
Iterate over all vertices to, that can be reached from v.
int to =
g[v][i];
if (to ==
p) continue;
dfs(to,v);
for(int x = 1; x <= k; x++)
dp[v][x] += dp[to][x-1];
}
}
The dfsRes function implements depth-first search
from vertex v with computing the
answer.
void dfsRes(int
v, int p = -1)
{
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (to ==
p) continue;
dfsRes(to,v);
for(int x = 1; x < k; x++)
resA += 1LL * dp[to][x-1] * (dp[v][k-x] -
dp[to][k-x-1]);
}
resB += dp[v][k];
}
The main part of the program. Read the input data. Construct a tree.
scanf("%d %d",&n,&k);
g.resize(n+1);
for(i = 0; i < n - 1; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
}
With the first depth-first search we construct the array dp.
dp.resize(n+1);
dfs(1);
Compute and print the answer.
resA = resB = 0;
dfsRes(1);
res = resA / 2 +
resB;
printf("%lld\n",res);